↓ 跳过正文
  1. Posts/

加密货币钱包技术解析：从助记词生成到地址派生的完整流程

·3913 字·8 分钟
CTF Misc Blockchain
目录

tl;dr

graph LR
    subgraph BIP39_助记词生成流程
        direction TB
        B1[随机熵生成] --> B2[计算校验和]
        B2 --> B3[组合熵+校验和]
        B3 --> B4[分割 11 位组]
        B4 --> B5[映射到词表]
        B5 --> B6[生成助记词]
    end
    subgraph PBKDF2_种子生成
        direction TB
        P1[助记词] --> P2["`盐 = 
        mnemonic + 密码`"]
        P2 --> P3["`PBKDF2
        2048次迭代`"]
        P3 --> P4[HMAC-SHA512]
        P4 --> P5[512位种子]
    end
    subgraph BIP32_HD钱包派生
        direction TB
        H1[主种子] --> H2[HMAC-SHA512]
        H2 --> H3[主私钥 + 链码]
        H3 --> H4[派生路径]
        H4 --> H5[CKD函数]
        H5 --> H6[子密钥对]
        H6 --> H7[钱包地址]
    end
BIP39_助记词生成流程 --> PBKDF2_种子生成
PBKDF2_种子生成 --> BIP32_HD钱包派生

Abstract
#

这篇博文系统性地阐述了现代加密货币（如比特币、以太坊）钱包的核心技术标准——BIP-39、BIP-32和BIP-44，详细揭示了从随机数开始直至生成钱包地址的全链条流程。

BIP-39 (生成助记词)
#

什么是 BIP-39
#

BIP-39 (Bitcoin Improvement Proposal 39)1本质是一套 将二进制随机数（熵，即钱包的主私钥）映射为人类可读单词 的编码方案

生成
#

它的生成过程可以分为两个主要阶段：

  1. 助记词生成(Mnemonic Generation)： 熵(Entropy) -> 助记词(Mnemonic)
  2. 种子生成(Seed Generation)： 助记词(Mnemonic) -> 二进制种子(Seed)

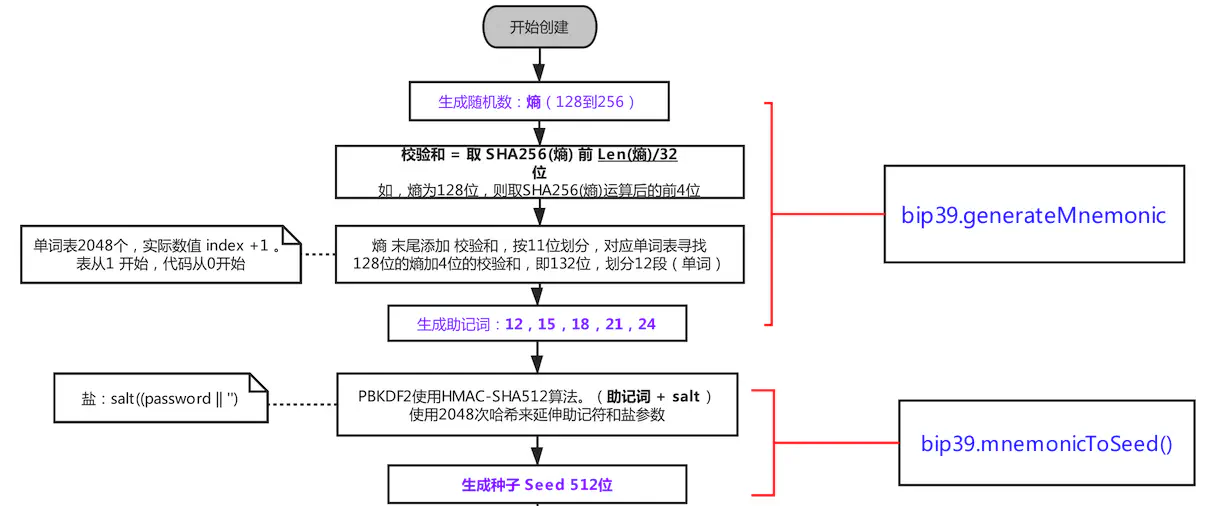
从熵生成助记词
#

  1. 生成熵 (Entropy)： 生成 $ENT$ 比特(bit)的随机序列，其中$ENT \in {128,160,192,224,256}$
    熵源需要在密码学上足够安全，不可预测、均匀分布，例如硬件熵源（haveged）或抛硬币结果
  2. 计算校验和 (Checksum)： 对熵进行 SHA-256 哈希，取哈希值的前 $CS$ 位，其中$CS = ENT/32 $
  3. 拼接： 将 熵 和 校验和 拼接，总长度变为$ENT+CS$ 位。
  4. 分割： 将这 $ENT+CS$ 位切分成 $MS=(ENT+CS)/11$ 段，每段 11 位。
    • 为什么是 11 位？因为 $2^{11} = 2048$，正好对应 BIP-39 标准词库中的 2048 个单词。
    • 这张表展示了长度之间的关系2
      ENTCSENT+CSMS
      128413212
      160516515
      192619818
      224723121
      256826424
  5. 映射： 将每段 11 位的二进制转换为十进制索引，在词库中查找对应的单词。
    ps: 词库有多个语言的版本
import hashlib
import binascii
from mnemonic import Mnemonic
mnemo = Mnemonic("english")
wordlist = mnemo.wordlist

def generate_mnemonic(entropy_hex):
    entropy_bytes = binascii.unhexlify(entropy_hex)
    entropy_bits = bin(int(entropy_hex, 16))[2:].zfill(len(entropy_bytes) * 8)
    hash_bytes = hashlib.sha256(entropy_bytes).digest()
    hash_bits = bin(int.from_bytes(hash_bytes, 'big'))[2:].zfill(256)
    checksum_len = len(entropy_bits) // 32
    checksum = hash_bits[:checksum_len]
    combined_bits = entropy_bits + checksum
    print(f"Combined Bits ({len(combined_bits)}): {combined_bits}")
    chunks = [combined_bits[i:i+11] for i in range(0, len(combined_bits), 11)]
    mnemonic = []
    for chunk in chunks:
        index = int(chunk, 2)
        mnemonic.append(wordlist[index])
    return " ".join(mnemonic)

print(generate_mnemonic('1f8a4ba31834374bf6c21bfecd63b718e26789139b52ed76cee5764dda23e0e9'))
# 'buzz false trip corn drop planet swallow drop yard help universe crack chapter setup example heart uniform reopen rich uncle tank ball lonely chimney'

根据助记词生成种子
#

有了助记词后，需要将其转化为 512 位的种子（Seed），用于生成私钥（BIP-32）。

  • 算法： PBKDF2(Password-Based Key Derivation Function 2) 密钥拉伸函数
  • 哈希函数： HMAC-SHA512
  • 密码： 助记词字符串
  • 盐 (Salt)： 字符串 “mnemonic” + 可选的 Passphrase (密码口令)（也叫“扩展密码”或“第 25 个词”）
  • 迭代次数： 2048 次
  • 输出种子长度： 512 位
import binascii
import hashlib

def generate_seed(mnemonic, passphrase=""):
    salt = ("mnemonic" + passphrase).encode('utf-8')
    # PBKDF2 with HMAC-SHA512, 2048 iterations
    seed = hashlib.pbkdf2_hmac(
        'sha512',
        mnemonic.encode('utf-8'),
        salt,
        2048
    )
    return binascii.hexlify(seed).decode('utf-8')

print(generate_seed('buzz false trip corn drop planet swallow drop yard help universe crack chapter setup example heart uniform reopen rich uncle tank ball lonely chimney'))
# a614e08e8e15ea54950a06948168b3be58b0ec3c2b10142a843279f0c0055fb2d74635bcbaa706794bf87dc9cbf7a1c959a9951233d4b2ea84f0d1d4a6912cb6

使用 mnemonic 库的代码实现：

from mnemonic import Mnemonic
mnemo = Mnemonic("english")
wordlist = mnemo.wordlist
words = mnemo.generate(strength=256)
print(words.split(" "))
# ['buzz', 'false', 'trip', 'corn', 'drop', 'planet', 'swallow', 'drop', 'yard', 'help', 'universe', 'crack', 'chapter', 'setup', 'example', 'heart', 'uniform', 'reopen', 'rich', 'uncle', 'tank', 'ball', 'lonely', 'chimney']
print(mnemo.check(words)) # 检验助记词校验和
# True
seed = mnemo.to_seed(words, passphrase="") # 助记词转seed
print(seed.hex())
# a614e08e8e15ea54950a06948168b3be58b0ec3c2b10142a843279f0c0055fb2d74635bcbaa706794bf87dc9cbf7a1c959a9951233d4b2ea84f0d1d4a6912cb6
entropy = mnemo.to_entropy(words) # 根据助记词计算原始熵
print(entropy.hex())
# '1f8a4ba31834374bf6c21bfecd63b718e26789139b52ed76cee5764dda23e0e9'

BIP-32 (分层钱包)
#

在 BIP-39 中，助记词通过 PBKDF2 函数变成了 512 位的 Seed。这个 Seed 是所有密钥的“祖先”。

BIP-32 (Hierarchical Deterministic Wallets) 定义了如何利用这个 Seed 生成一个 主私钥 (Master Private Key) 和 链码 (Chain Code)，即如何从一个种子生成一个树状结构的密钥体系（主私钥 -> 子私钥 -> 孙私钥…）。它规定了扩展密钥的概念，可以从一个父密钥派生出海量的子密钥，而无需备份每一个。

从种子到主扩展私钥
#

将上一步 BIP-39 得到的种子作为输入，再次使用 HMAC-SHA512 算法进行计算，通常以字符串 “Bitcoin seed” 作为 Key，种子作为 Data。

输出的 512 比特 结果分为两部分：

  • 前 256 比特：作为 主私钥（Master，$m$）
  • 后 256 比特：作为 主链码（Master chain code）

主私钥 + 主链码 一起构成了 BIP32 定义的 主扩展私钥。从这个根上，可以派生出一整棵密钥树。

BIP-44 (派生路径)
#

路径格式
#

BIP44(多币种分层确定性钱包结构) 基于 BIP32 的树状结构，定义了一种标准化的路径格式：

$$ m/purpose'/coin\_type'/account'/change/address\_index $$

其中：

  • $m$: 主私钥
  • $purpose’$: 协议版本 (44’代表 BIP-44, 49’代表 SegWit(BIP-49), 84’代表 Native-SegWit(BIP-84))

    Keys derivation as defined by:3

    Derivation of a hierarchy of keys as defined by:

  • $coin type’$: 币种 (0’是比特币, 60’是以太坊，其他参见SLIP-0044)
  • $account’$: 账户索引 (从0’开始递增，它允许用户在一个钱包内管理多个独立账户)
  • $change$: 找零标识，0 代表对外收款地址，1 代表找零地址
  • $address index$: 地址索引 (0, 1, 2…)
    官方建议每个account下的address_index不要超过20

注意： 带 ' 号表示 硬化派生 (Hardened Derivation)。这是一种安全机制，防止子公钥泄露导致父私钥被破解。硬化派生使用父私钥推导，索引号在$2^{31}$到$2^{32}-1$之间，而常规派生使用父公钥推导，索引号在$0$到$2^{31}$之间

例如，比特币第一个账户的第一个接收地址路径为：m/44’/0’/0’/0/0
这个路径就像文件夹目录，让不同的币种、账户、找零地址都能有组织地存放在确定的位置


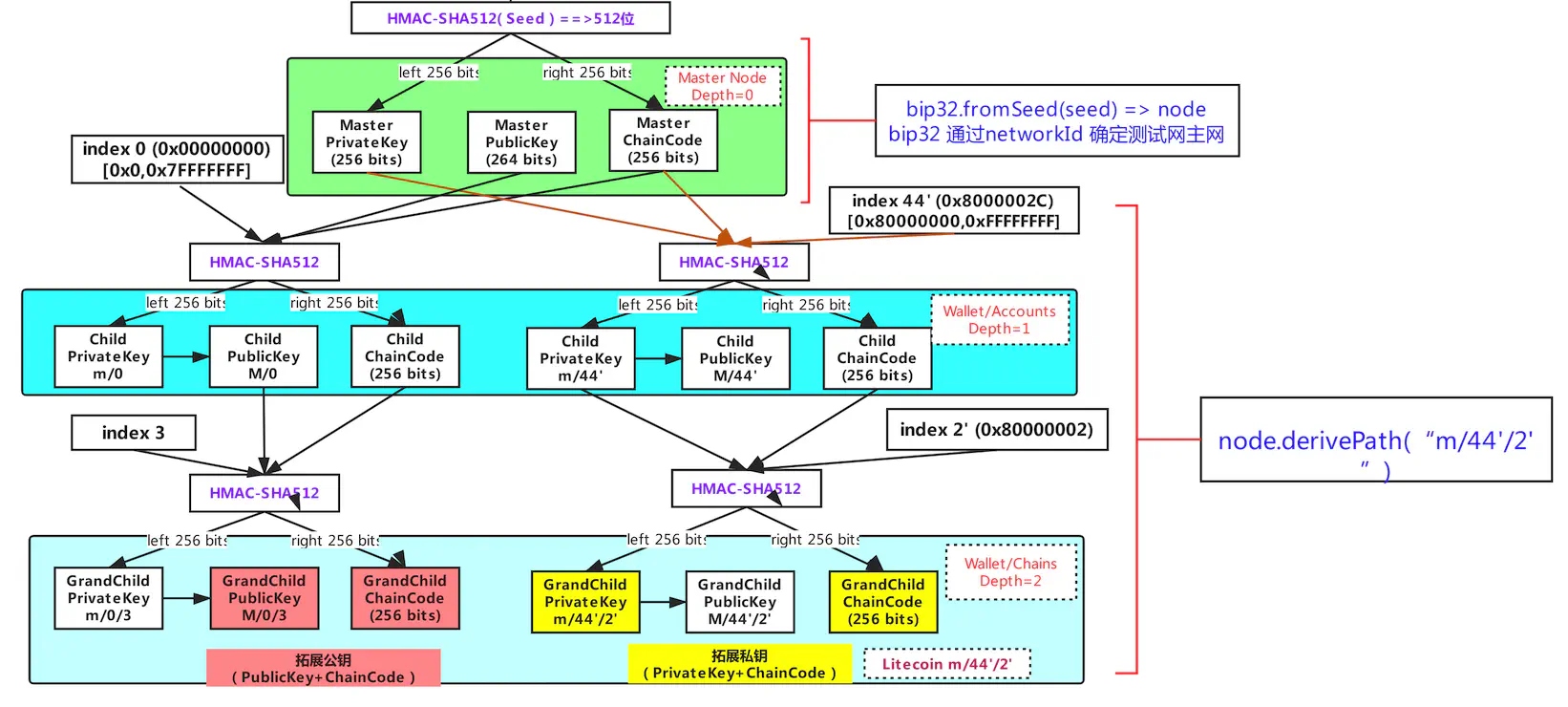
通过增加索引（水平扩展）及 通过子秘钥向下一层（深度扩展）可以无限生成私钥。

level0 (root)
  └── level1 (purpose)
        └── level2 (coin_type)
              └── level3 (account)
                    └── level4 (parent)
                          └── level5 (child)
                                └── level6 (grandchild)
                                      └── ...

派生私钥
#

与前面的从种子到主扩展私钥类似的，派生私钥使用 CKD(child key derivation) 函数从父密钥(parent keys)推导子密钥(child keys)，CKD 由下列三个要素做单向散列哈希（HMAC-SHA512等）：

  • 父密钥(ParentPrivateKey)：没有压缩过的椭圆曲线推导的私钥或公钥(ECDSA uncompressed key)
  • 链码(ParentChainCode)：256比特熵
  • 子索引序号(i)32比特
$$I = \text{HMAC-SHA512}(Key=ParentChainCode, Data=InputData)$$


结果 $I$ 是 512 位的，分为左 256 位 ($I_L$) 和右 256 位 ($I_R$)。
生成子扩展私钥和子链码。

  • 子私钥 (ChildPrivateKey): $(I_L + ParentPrivateKey) \mod n$
  • 子链码 (ChildChainCode): 直接等于 $I_R$

这个推导过程是单射的，子密钥不能推导出同层级的兄弟密钥，也不能推出父密钥。如果没有子链码也不能推导出孙密钥。

E.g. 从主扩展私钥派生父私钥
#

使用bip32utils（过时）

import binascii
from bip32utils import BIP32Key
BIP32_HARDEN = 0x80000000 # 定义硬化索引偏移量
seed = binascii.unhexlify('a614e08e8e15ea54950a06948168b3be58b0ec3c2b10142a843279f0c0055fb2d74635bcbaa706794bf87dc9cbf7a1c959a9951233d4b2ea84f0d1d4a6912cb6')
root = BIP32Key.fromEntropy(seed)
# 推导路径: m/44'/60'/0'/0
parent = root.ChildKey(44 + BIP32_HARDEN) \
             .ChildKey(60 + BIP32_HARDEN) \
             .ChildKey(0 + BIP32_HARDEN) \
             .ChildKey(0)
print("Parent private key:", parent.PrivateKey().hex())
# 9809d91a09569437f52c04d2540d7c91eaea42e3df5787ffe108b5444a1f10e3
print("Parent private key extended:", parent.ExtendedKey())
# 'xprv9s21ZrQH143K24Mfq5zL5MhWK9hUhhGbd45hLXo2Pq2oqzMMo63oStZzFACVhq1bBacvYpuDvaSc5z1L16nL1ee5BgCdBD7m3Pm3n4HY2AK'

使用bip_utils

import binascii
from bip_utils import Bip44, Bip44Coins, Bip44Changes
seed = binascii.unhexlify("a614e08e8e15ea54950a06948168b3be58b0ec3c2b10142a843279f0c0055fb2d74635bcbaa706794bf87dc9cbf7a1c959a9951233d4b2ea84f0d1d4a6912cb6")
root = Bip44.FromSeed(seed, Bip44Coins.ETHEREUM)
# m/44'/60'/0'/0
parent = root.Purpose().Coin().Account(0).Change(Bip44Changes.CHAIN_EXT)
print("Parent private key:", parent.PrivateKey().Raw().ToHex())
# 9809d91a09569437f52c04d2540d7c91eaea42e3df5787ffe108b5444a1f10e3
print("Parent private key extended:", parent.PrivateKey().ToExtended())
# xprvA1YS8AZAANo7vn3agrsNtgPaN7hR8LeT4a6kxtZuSr1rz5bHZUecJ8n4fKeDuVf1pmWyTcCHLahV3d5FxMiPmjiAw7k7XkgSs7CfoD7thfs

E.g. 从父私钥派生子私钥
#

使用bip32utils

import binascii
from bip32utils import BIP32Key
parent = BIP32Key.fromExtendedKey('xprv9s21ZrQH143K24Mfq5zL5MhWK9hUhhGbd45hLXo2Pq2oqzMMo63oStZzFACVhq1\
bBacvYpuDvaSc5z1L16nL1ee5BgCdBD7m3Pm3n4HY2AK')
# m/44'/60'/0'/0/5
child = parent.ChildKey(5)
print("Child private key:", child.PrivateKey().hex())
# 1bcd2c630201a1aedfb9febda4926e68be810c2eada4cde11d3180211de78d56
# m/44'/60'/0'/0/5/3
grandchild = child.ChildKey(3)
print("Grandchild private key:", grandchild.PrivateKey().hex())
# db2d0dab8c23074abe8c5e6ea0f87e2e28e021b6fb716717e4da05379ed98e4e

使用bip_utils

from bip_utils import Bip32Slip10Secp256k1
parent = Bip32Slip10Secp256k1.FromExtendedKey('xprv9s21ZrQH143K24Mfq5zL5MhWK9hUhhGbd45hLXo2Pq2oqzMMo63oStZzFACVhq1\
bBacvYpuDvaSc5z1L16nL1ee5BgCdBD7m3Pm3n4HY2AK')
# m/44'/60'/0'/0/5
child = parent.DerivePath("m/5")
print("Child private key:", child.PrivateKey().Raw())
# 1bcd2c630201a1aedfb9febda4926e68be810c2eada4cde11d3180211de78d56
# m/44'/60'/0'/0/5/3
grandchild = parent.DerivePath("m/5/3")
print("Grandchild private key:", grandchild.PrivateKey().Raw())
# db2d0dab8c23074abe8c5e6ea0f87e2e28e021b6fb716717e4da05379ed98e4e

生成公钥
#

graph LR
    k("`私钥
    k`") -->|椭圆曲线相乘（单向）| KK("`公钥
    P`")
    KK -->|哈希函数（单向）| A("`比特币地址
    A`")
    A -->|不可逆| KK
    KK -->|不可逆| k

k，私钥，通常是随机产生，需要绝对保密的
P，公钥，由私钥通过椭圆曲线乘法运算而来，不可倒推出私钥，可以不保密
A，地址，由公钥通过单向哈希运算而来，不可倒推出公钥，是完全公开的

私钥是一个随机的大整数 $k$，公钥是椭圆曲线上的一个点 $P$。关系为：

$$P = k \times G$$


其中 $G$ 是椭圆曲线的基点。这一步是单向的，无法逆推。

使用椭圆曲线加密算法（比特币是secp256k1），将上一步得到的最终私钥进行数学运算，生成对应的公钥（一个65字节未压缩或33字节压缩的坐标点）。现代钱包通常使用压缩公钥（33字节）。

import binascii
from bip_utils import Bip44, Bip44Coins, Bip44Changes
grandchild = Bip44.FromPrivateKey(binascii.unhexlify("db2d0dab8c23074abe8c5e6ea0f87e2e28e021b6fb716\
717e4da05379ed98e4e"),Bip44Coins.ETHEREUM)
print(grandchild.PublicKey().RawCompressed())
# 037faa9191249e2c78d56cb930440956b797b6da064660aef6d463f2703563c220
print(grandchild.PublicKey().RawUncompressed())
# 047faa9191249e2c78d56cb930440956b797b6da064660aef6d463f2703563c22054a9e9ac7b1668fff3d762cfcda39ffabd609733d0bec4200d5c84b3739cebc1

生成地址
#

以太坊地址生成 (Hex)
#

  1. 对 非压缩公钥 (移除 04 前缀后) 进行 Keccak-256 哈希
  2. 取哈希值的最后 20 字节
  3. 转为十六进制，并在前面加 0x
  4. (可选但重要) EIP-55 校验: 对地址中的字母进行大小写转换以充当校验和
import binascii
from bip_utils import Bip44, Bip44Coins, Bip44Changes
grandchild = Bip44.FromPrivateKey(binascii.unhexlify("db2d0dab8c23074abe8c5e6ea0f87e2e28e021b6fb716\
717e4da05379ed98e4e"),Bip44Coins.ETHEREUM)
print(grandchild.PublicKey().ToAddress())
# 0x6eB19F869226D6C62b5421Ab1b42890cF209f4D1

比特币地址生成 (Base58Check)
#

  1. 对公钥进行一次SHA-256哈希
  2. 对上一步结果进行 RIPEMD-160 哈希（得到 20 字节指纹）
  3. 给指纹加上版本前缀（例如比特币主网是 0x00）
  4. 对 (版本前缀+指纹) 进行两次 SHA-256，取前 4 字节作为校验和
  5. 拼接 版本前缀 + 指纹 + 校验和
  6. 对结果进行 Base58 编码
import binascii
from bip_utils import Bip44, Bip44Coins, Bip44Changes
grandchild = Bip44.FromPrivateKey(binascii.unhexlify("..."),Bip44Coins.BITCOIN)
print(grandchild.PublicKey().ToAddress())

CTF 实战
#

助记词残缺
#

2025 第八届浙江省大学生网络与信息安全竞赛 初赛
misc 5-2 RecoverWallet
已知信息：

  1. 助记词（缺少第五个）
    ["ankle", "assume", "estate", "permit", None, "eye", "fancy", "spring", "demand", "dial", "awkward", "hole"]
  2. 钱包地址后缀 700f80

求：

  • 钱包地址

爆破一下就好了

伪随机数生成器 (PRNG) 预测
#

题目： 提供了一个生成助记词的 Python 脚本，但使用了 random.seed(time.time()) 或者不安全的随机源。

分析： BIP-39 的安全性完全依赖于 熵 的不可预测性。如果攻击者能预测熵（Entropy），就能生成一模一样的助记词。如果题目代码使用了当前时间戳作为随机数种子，我们可以爆破题目生成时的秒数（Unix Timestamp），复现出当时的 Entropy。

思路：

  • 分析代码找到随机种子来源（如时间戳）。
  • 估算题目生成的大致时间范围。
  • 遍历时间戳，生成 Entropy，转换为助记词。
  • 比对公钥/地址是否匹配。

非标准路径或自定义词库
#

题目： 给了完整的助记词，但导入常规钱包（如 MetaMask）后余额为 0，而题目暗示确有资产。
分析：

  1. Passphrase (Salt) 隐写： 用户可能设置了额外的 Passphrase。这是 BIP-39 的一部分，会导致生成完全不同的种子。CTF 中可能需要对 Passphrase 进行字典攻击。
  2. Derivation Path (BIP-44)： 相同的种子，在不同的推导路径下会产生不同的私钥。
    比特币标准：m/44'/0'/0'/0/0
    以太坊标准：m/44'/60'/0'/0/0
    题目可能使用了怪异的路径，如 m/44'/1337'/...。
    思路：尝试修改 account 或 address_index，遍历可能路径，

扩展公钥 (Extended Public Key, XPUB) 泄露
#

如果在题目中拿到了 xpub (扩展公钥)，可以推导出该账户下所有的子公钥和地址，查看所有交易记录。
更危险的是，如果泄露了 xpub 以及 任意一个子私钥，根据椭圆曲线的数学特性，攻击者可以反向计算出 主私钥 (xprv)。这是一个高阶的 Crypto 考点。

  1. https://en.wikipedia.org/wiki/Cryptocurrency_wallet#Hierarchical_deterministic_wallet ↩︎

  2. https://fpchen.readthedocs.io/zh/latest/note/BlockChain/wallet/BIP39-BIP32-BIP44.html#bip39 ↩︎

  3. https://pypi.org/project/bip-utils/ ↩︎

Timmy
作者
Timmy
Fighting for Love.

相关文章

第八届浙江省大学生网络与信息安全竞赛 决赛 WriteUp
·169 字·1 分钟
CTF WriteUps 浙江
第八届浙江省大学生网络与信息安全竞赛 初赛 WriteUp
·1724 字·4 分钟
CTF WriteUps 浙江
?CTF 2025 WriteUp
·6009 字·12 分钟
CTF WriteUps